Benchmarking methods for identification of DE genes between discrete cell types
Introduction
In this example, we will demonstrate how to use scDesign3Py to generate negative control and benchmark methods for identifying differentially expressed (DE) genes between discrete cell types. Please note that here we only did a very brief benchmarking for illustration purpose, not for formal comparison.
Import packages and Read in data
import pacakges
import anndata as ad
import numpy as np
import pandas as pd
import scanpy as sc
import scDesign3Py
Read in data
The raw data is from the R package DuoClustering2018, which contain a set of datasets with various clustering results and converted to .h5ad file using the R package sceasy.
data = ad.read_h5ad("data/Zhengmix4eq.h5ad")
The top 200 highly variable genes are kept for generating synthetic data.
data.layers["log"] = data.X.copy()
sc.pp.normalize_total(data,target_sum=1e4,layer="log")
sc.pp.log1p(data,layer="log")
# choose HVG genes
sc.pp.highly_variable_genes(data,layer="log",n_top_genes=200)
data = data[:,data.var["highly_variable"] == True]
We extract out B cells and regulatory T cells only and use all cells from these two cell types to simulate synthetic data.
data = data[(data.obs["phenoid"]=="b.cells")|(data.obs["phenoid"]=="regulatory.t"),:]
data.obs["cell_type"] = data.obs["phenoid"]
data
AnnData object with n_obs × n_vars = 1802 × 200
obs: 'barcode', 'phenoid', 'total_features', 'log10_total_features', 'total_counts', 'log10_total_counts', 'pct_counts_top_50_features', 'pct_counts_top_100_features', 'pct_counts_top_200_features', 'pct_counts_top_500_features', 'sizeFactor', 'cell_type'
var: 'id', 'symbol', 'mean_counts', 'log10_mean_counts', 'rank_counts', 'n_cells_counts', 'pct_dropout_counts', 'total_counts', 'log10_total_counts', 'highly_variable', 'means', 'dispersions', 'dispersions_norm'
uns: 'log1p', 'hvg'
obsm: 'X_pca', 'X_tsne'
layers: 'logcounts', 'normcounts', 'log'
data.obs["cell_type"].head()
b.cells6276 b.cells
b.cells6144 b.cells
b.cells6285 b.cells
b.cells8679 b.cells
b.cells96 b.cells
Name: cell_type, dtype: category
Categories (2, object): ['b.cells', 'regulatory.t']
Simulation
We use the step-by-step functions instead of the one-shot function to generate synthetic data since these step-by-step functions allow us to alter estimated parameters and generate new data based on our desired parameters.
example = scDesign3Py.scDesign3(n_cores=3,parallelization="pbmcmapply")
example_data = example.construct_data(
anndata = data,
default_assay_name = "counts",
celltype = "cell_type",
corr_formula = "1")
example.set_r_random_seed(123)
example_marginal = example.fit_marginal(
mu_formula = "cell_type",
sigma_formula = "1",
family_use = "nb",
usebam = False
)
example.set_r_random_seed(123)
example_copula = example.fit_copula()
example_para = example.extract_para()
Here, we examine the mean_mat, which is one of the outputs from the previous function extract_para(). For each gene, we calculate the difference in the between the maximum mean parameter and minimum mean parameter across all cells. We select genes which the gene’s mean difference across cells are in the top 50 largest differences. We regard these genes as DE genes. Then, we manually set the mean parameters of the rest genes to be the same across all cells. We regard all genes with the same mean parameter across cells as non-DE genes. Of course, this is a very flexible step and users may choose other ideas to modify the mean matrix.
diff_idx = (example_para["mean_mat"].max() - example_para["mean_mat"].min()).sort_values(ascending=False).index
de_idx = diff_idx[:50]
no_de_idx = diff_idx[50:]
example_para["mean_mat"][no_de_idx] = ((example_para["mean_mat"].max() + example_para["mean_mat"].min())/2)[no_de_idx]
example.set_r_random_seed(123)
example_newcount = example.simu_new(mean_mat=example_para["mean_mat"])
DE genes identification
Then, we follow Scanpy’s pipeline to preprocess the simulated data.
simu_data = ad.AnnData(example_newcount)
simu_data.var["mt"] = simu_data.var_names.str.startswith("MT-")
sc.pp.calculate_qc_metrics(
simu_data, qc_vars=["mt"], percent_top=None, log1p=False, inplace=True
)
simu_data = simu_data[simu_data.obs.n_genes_by_counts < 2500, :]
simu_data = simu_data[simu_data.obs.pct_counts_mt < 5, :].copy()
sc.pp.normalize_total(simu_data, target_sum=1e4)
sc.pp.log1p(simu_data)
simu_data.raw = simu_data
sc.pp.scale(simu_data, max_value=10)
Since we already have the ground truth cell type annotations for our simulated dataset, we can directly use the cell type annotations we have instead of clustering manually.
simu_data.obs["cell_type"] = data.obs["cell_type"]
We follow Scanpy’s pipeline to conduct DE test.
Here, we only benchmark t test and wilcoxon test as an example.
qvals = pd.DataFrame(index=simu_data.var_names)
methods = ["t-test","wilcoxon"]
for method in methods:
sc.tl.rank_genes_groups(simu_data, "cell_type", method=method, use_raw=True)
tmp = pd.DataFrame(simu_data.uns["rank_genes_groups"]["pvals_adj"]["b.cells"],index=simu_data.uns["rank_genes_groups"]["names"]["b.cells"],columns=[method])
qvals = pd.concat([qvals,tmp],axis=1)
Since we manually created non-DE genes in the extra_para() step, now we can calculate the actual false discovery proportion(FDP) and power of the DE tests we conducted above with various target FDR threshold.
targetFDR = np.concatenate([np.arange(0.01,0.11,0.01),np.arange(0.2,0.6,0.1)])
fdp = pd.DataFrame(index=targetFDR,columns=methods)
power = pd.DataFrame(index=targetFDR,columns=methods)
for method in methods:
curr_p = qvals[method]
for threshold in targetFDR:
discovery = curr_p[curr_p <= threshold]
true_positive = discovery.index.intersection(de_idx).shape[0]
if len(discovery) == 0:
fdp.loc[threshold,method] = 0
else:
fdp.loc[threshold,method] = (len(discovery) - true_positive)/len(discovery)
power.loc[threshold,method] = true_positive/de_idx.shape[0]
Visualization
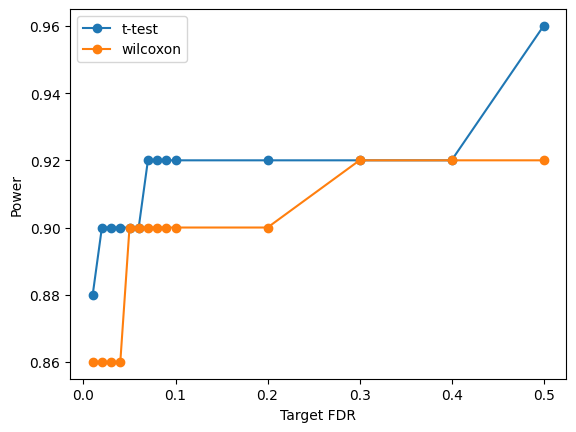
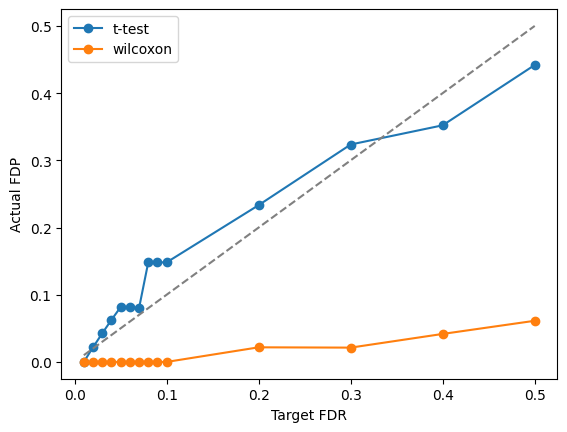
We visualize the Target FDR vs Actual FDP and Target FDR vs Power below.
import matplotlib.pyplot as plt
Show code cell source
for method in methods:
plt.plot(targetFDR,fdp[method],"o-",label=method)
plt.plot(targetFDR, targetFDR, '--', color='gray')
plt.xlabel('Target FDR')
plt.ylabel('Actual FDP')
plt.legend(loc="best")
plt.show()
Show code cell source
for method in methods:
plt.plot(targetFDR,power[method],"o-",label=method)
plt.xlabel('Target FDR')
plt.ylabel('Power')
plt.legend(loc="best")
plt.show()