Simulate spatial transcriptomic data

Introduction

In this example, we show how to use scDesign3Py to simulate the spot-resolution spatial data, which each spot is a mix of cells from different cell types.

Import packages and Read in data

import pacakges

import anndata as ad
import pandas as pd
import numpy as np
import scDesign3Py

import cell2location

Read in the reference data

The paired scRNA-seq and spatial data were used in CARD. We pre-select the top cell-type marker genes.

MOBSC_exp = ad.read_h5ad("data/MOBSC.h5ad")
MOBSP_exp = ad.read_h5ad("data/MOBSP.h5ad")

MOBSC_exp

AnnData object with n_obs × n_vars = 12640 × 182
    obs: 'cellType', 'sampleInfo', 'sizeFactor', 'cell_type'
    var: 'rownames.count.'

MOBSP_exp

AnnData object with n_obs × n_vars = 278 × 182
    obs: 'spatial1', 'spatial2'
    var: 'name'

cell_type = MOBSC_exp.obs["cellType"].unique()

Simulation

We first use scDesign3Py to estimate the cell-type reference from scRNA-seq data.

mobsc = scDesign3Py.scDesign3(n_cores=3,parallelization="pbmcmapply")
mobsc.set_r_random_seed(123)
MOBSC_data = mobsc.construct_data(
    anndata=MOBSC_exp,
    default_assay_name="counts",
    celltype="cell_type",
    corr_formula="1"
)
MOBSC_marginal = mobsc.fit_marginal(  
    mu_formula = "cell_type",
    sigma_formula = "cell_type",
    family_use="nb",
    usebam=False
)
MOBSC_copula = mobsc.fit_copula()
MOBSC_para = mobsc.extract_para()
MOBSC_newcount = mobsc.simu_new()

mobsp = scDesign3Py.scDesign3(n_cores=3,parallelization="pbmcmapply")
mobsp.set_r_random_seed(123)
MOBSP_data = mobsp.construct_data(
    anndata=MOBSP_exp,
    default_assay_name="counts",
    spatial=["spatial1", "spatial2"],
    corr_formula="1"
)
MOBSP_marginal = mobsp.fit_marginal(  
    mu_formula = "s(spatial1, spatial2, bs = 'gp', k = 50, m = c(1, 2, 1))",
    sigma_formula = "1",
    family_use="nb",
    usebam=False
)
MOBSP_copula = mobsp.fit_copula()
MOBSP_para = mobsp.extract_para()

Deconvolution

Now we get the fitted models for scRNA-seq and spatial data. We need to extract their mean parameters (i.e., expected expression values).

MOBSC_sig_matrix = pd.DataFrame(index = MOBSC_para["mean_mat"].columns)
for t in cell_type:
    cell = MOBSC_exp.obs[MOBSC_exp.obs["cell_type"]==t].index
    MOBSC_sig_matrix[t] = MOBSC_para["mean_mat"].loc[cell,:].mean().T
mixture_file = ad.AnnData(MOBSP_para["mean_mat"])
mixture_file.X = np.round(mixture_file.X)

We use cell2location to decompose each spot’s expected expression into cell-type proportions. This step is to set the true cell-type proportions. Please note you can also use other decomposition methods or set the proportion mannully if you have your own design.

cell2location.models.Cell2location.setup_anndata(adata=mixture_file)
mod = cell2location.models.Cell2location(
    adata = mixture_file,
    cell_state_df=MOBSC_sig_matrix,
)
mod.train(max_epochs=1000)
mixture_file = mod.export_posterior(mixture_file, sample_kwargs={"num_samples":1000, "batch_size":mod.adata.n_obs,"use_gpu":True})

Then we can simulate new spatial data where each spot is the sum of 50 cells/5 (therefore on average 10 cells per spot). Increasing the number of cells will make the spatial data smoother (closer to the expected spatial expression).

abundance = mixture_file.obsm['q05_cell_abundance_w_sf']
abundance.columns = cell_type
percent = abundance.div(abundance.sum(axis=1), axis=0)

# simu single cell data
simu_data = ad.AnnData(X=MOBSC_newcount,obs=MOBSC_exp.obs)

# simu mixture data
mixture = []
for spot in MOBSP_exp.obs_names:
    n = 50
    count = pd.Series(0,index=MOBSC_exp.var_names)
    for t in cell_type:
        tmp = simu_data[simu_data.obs["cell_type"]==t, ]
        index = tmp.obs.sample(n=n).index
        count_t = MOBSC_newcount.loc[index, ].sum() * percent.loc[spot,t]
        count = count + count_t
    count.name = spot
    mixture.append(count)
mixture = pd.concat(mixture,axis=1).T
mixture = mixture / 5
mixture = np.ceil(mixture)

simu_mixture = ad.AnnData(X=mixture, obs=MOBSP_exp.obs)

Visualization

import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib.patches import Patch

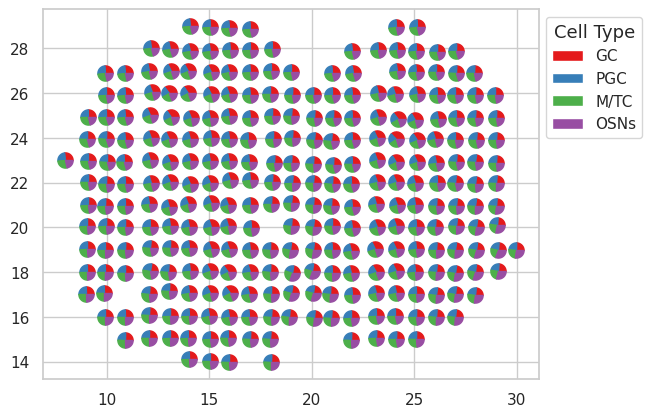
We can visualzie the proportions by pie-chart.

../../_images/c7fa1dd8767939f7a047cf54ac405cfdab0478485e657ab659d108a1c866d815.png

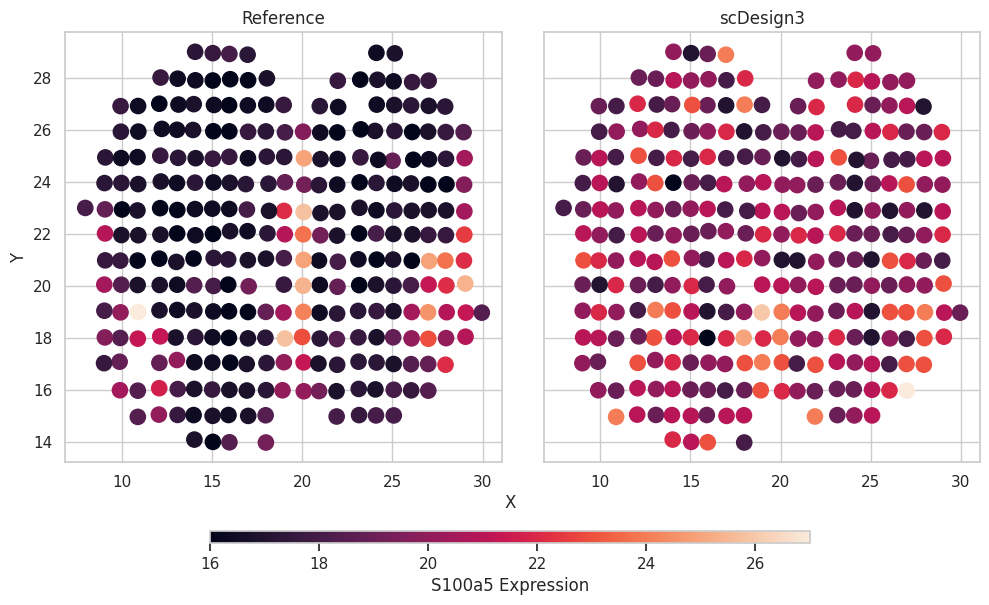
We can also check the simulated results. We use one cell-type marker genes as the example.

../../_images/53055e47cc6a8afac59ecd1c8834e6fcbd82957574d8d747fc0abefd542c68ea.png