Simulate datasets with multiple lineages

Introduction

In this example, we will show how to use scDesign3Py to simulate multiple lineages single-cell data.

Import packages and Read in data

import pacakges

import anndata as ad
import numpy as np
import scDesign3Py

Read in the reference data

The raw data is from the GEO with ID GSE72859, which describes myeloid progenitors from mouse bone marrow.

We pre-select the top 1000 highly variable genes. To save time, we only use the top 30 genes.

data = ad.read_h5ad("data/MARROW.h5ad")
data = data[:,0:30]
data

View of AnnData object with n_obs × n_vars = 2660 × 30
    obs: 'Seq_batch_ID', 'Amp_batch_ID', 'well_coordinates', 'Plate_ID', 'Pool_barcode', 'Cell_barcode', 'CD34_measurement', 'FcgR3_measurement', 'cluster', 'Size_Factor', 'cell_type', 'Pseudotime', 'State', 'cell_type2', 'ery_meg_lineage_score', 'cell_stemness_score', 'no_expression', 'sizeFactor', 'pseudotime1', 'pseudotime2', 'l1', 'l2'
    var: 'gene_short_name'
    obsm: 'X_umap'

As we can see, this example dataset has two sets of pseudotime, thus two lineages. The variables pseudotime1 and pseudotime2 contain the corresponding pseudotime for each cell. The variables l1 and l2 indicate whether a particular cell belong to the first and/or second lineages.

data.obs[["pseudotime1","pseudotime2","l1","l2"]].head()

	pseudotime1	pseudotime2	l1	l2
W31105	0.950862	0.568357	TRUE	TRUE
W31106	9.168276	-1.000000	TRUE	FALSE
W31107	-1.000000	7.981990	FALSE	TRUE
W31108	11.394132	-1.000000	TRUE	FALSE
W31109	-1.000000	8.080133	FALSE	TRUE

Simulation

Then, we can use this multiple-lineage dataset to generate new data by setting the parameter mu_formula as two smooth terms for each lineage.

test = scDesign3Py.scDesign3(n_cores=3,parallelization="pbmcmapply")
test.set_r_random_seed(123)
simu_res = test.scdesign3(
    anndata=data,
    default_assay_name="counts",
    celltype="cell_type",
    pseudotime=["pseudotime1", "pseudotime2", "l1", "l2"],
    mu_formula="s(pseudotime1, k = 10, by = l1, bs = 'cr') + s(pseudotime2, k = 10, by = l2, bs = 'cr')",
    sigma_formula="1",
    family_use="nb",
    usebam=False,
    corr_formula="1",
    copula="gaussian",
)

Then we can construct new data using the simulated count matrix.

simu_data = ad.AnnData(X=simu_res["new_count"], obs=simu_res["new_covariate"])
simu_data.layers["log_transformed"] = np.log1p(simu_data.X)
data.layers["log_transformed"] = np.log1p(data.X)

Visualization

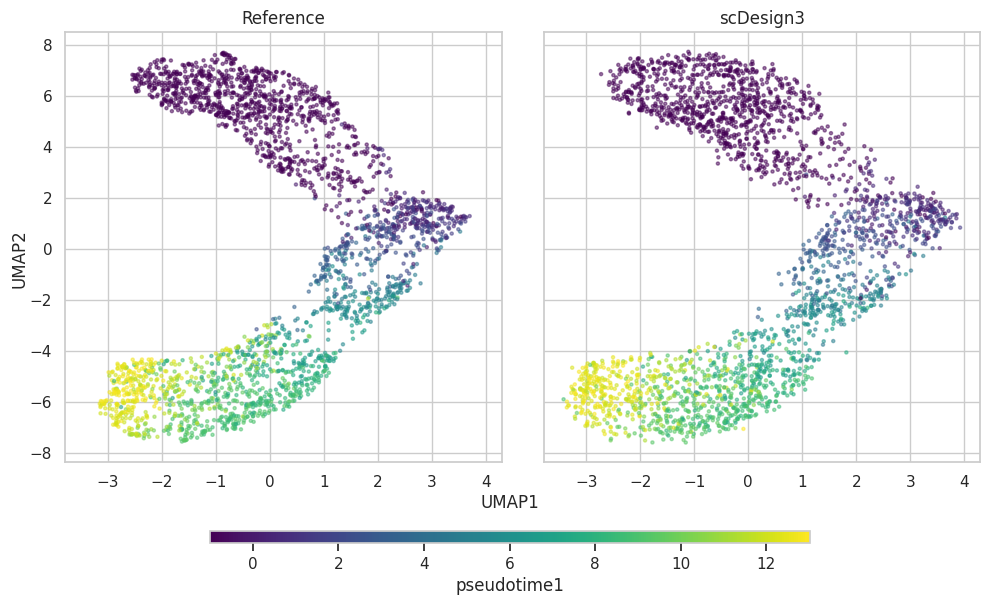
plot1 = scDesign3Py.plot_reduceddim(
    ref_anndata=data,
    anndata_list=simu_data,
    name_list=["Reference", "scDesign3"],
    assay_use="log_transformed",
    if_plot=True,
    color_by="pseudotime1",
    n_pc=20,
    point_size=5,
)
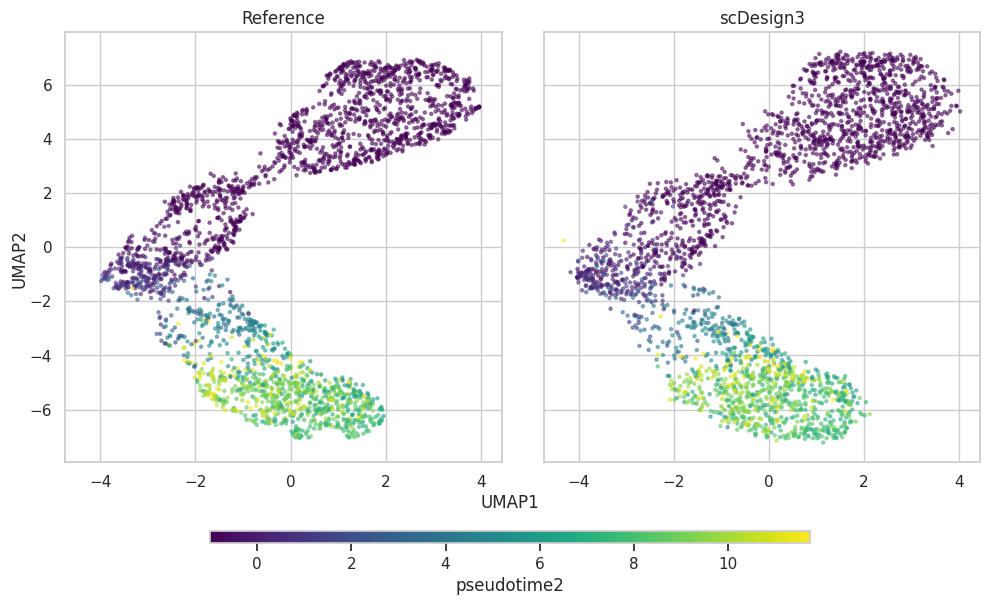
plot2 = scDesign3Py.plot_reduceddim(
    ref_anndata=data,
    anndata_list=simu_data,
    name_list=["Reference", "scDesign3"],
    assay_use="log_transformed",
    if_plot=True,
    color_by="pseudotime2",
    n_pc=20,
    point_size=5,
)

Pseudotime1

plot1["p_umap"]

Pseudotime2

plot2["p_umap"]